Thủ Thuật Hướng dẫn Câu 35 cho hình lăng trụ đứng có đáy là tam giác vuông tại tính góc giữa đường thẳng và mặt phẳng 2022
Họ và tên học viên Nữ đang tìm kiếm từ khóa Câu 35 cho hình lăng trụ đứng có đáy là tam giác vuông tại tính góc giữa đường thẳng và mặt phẳng được Cập Nhật vào lúc : 2022-05-03 15:25:52 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
LIVESTREAM 2K4 ÔN THI THPT QUỐC GIA 2022
[embed]https://www.youtube.com/watch?v=zFU8c40y7lU[/embed]
Nội dung chính- Cho hình lăng trụ đứng có đáylà tam giác vuông tại , , mặt phẳng tạo với đáy một góc và tam giác có diện tích s quy hoạnh bằng . Tínhthểtíchkhốilăngtrụ.
Bài tập trắc nghiệm 60 phút Thể tích khối lăng trụ. - Khối đa diện và thể tích - Toán Học 12 - Đề số 4Video liên quan
ĐỀ MINH HỌA CUỐI KÌ 2 HAY NHẤT - 2k5 - Livestream HÓA cô THU
Hóa học
[embed]https://www.youtube.com/watch?v=PBpe14ApvlA[/embed]
ĐỀ KIỂM TRA CUỐI KỲ 2 TRƯỜNG THPT NGÔ GIA TỰ - 2k6 - Livestream TOÁN thầy ANH TUẤN
Toán
[embed]https://www.youtube.com/watch?v=Bd19awtfFu8[/embed]
CHỮA ĐỀ THI VÀO 10 - ĐỀ TRÚNG TỦ 03 - 2k7 - Livestream TOÁN thầy QUANG HUY
Toán
[embed]https://www.youtube.com/watch?v=Z9PnhliqsW4[/embed]
CHỮA ĐỀ MINH HỌA THI CUỐI HỌC KÌ 2 (tiếp) - 2k5 Livestream TIẾNG ANH cô QUỲNH TRANG
Tiếng Anh (mới)
[embed]https://www.youtube.com/watch?v=ZCP0qIDC3mo[/embed]
ĐỀ MINH HỌA CUỐI HỌC KÌ 2 - 2K5 - Livestream HÓA cô HUYỀN
Hóa học
Xem thêm ...
Cho hình lăng trụ đứng (ABC.A'B'C') có đáy (ABC) là tam giác vuông tại (B), (BC = a), mặt phẳng (left( A'BC right)) tạo với đáy một góc (30^circ ) và tam giác (A'BC) có diện tích s quy hoạnh bằng (a^2sqrt 3 ). Tính thể tích khối lăng trụ (ABC.A'B'C').
A.
(dfrac3a^3sqrt 3 2)
B.
(dfrac3a^3sqrt 3 8)
C.
(dfraca^3sqrt 3 8)
D.
(dfrac3a^3sqrt 3 4)
Trang chủ
Sách ID
Khóa học miễn phí
Luyện thi ĐGNL và ĐH 2023
Cho hình lăng trụ đứng có đáylà tam giác vuông tại , , mặt phẳng tạo với đáy một góc và tam giác có diện tích s quy hoạnh bằng . Tínhthểtíchkhốilăngtrụ.
A.
B.
C.
D.
Đáp án và lời giải
Đáp án:D
Lời giải:
Phântích: V= Bh = SABC.A’B’C’.AA’. Do
. Và
Ta có: 
.
.
Vậy đáp án đúng là D.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Thể tích khối lăng trụ. - Khối đa diện và thể tích - Toán Học 12 - Đề số 4
Làm bài
Chia sẻ
Một số thắc mắc khác cùng bài thi.
Tổng diện tích s quy hoạnh những mặt của một hình lập phương là
. Thể tích khối lập phương là ?
Cho khối hộp chữ nhật
có 
. Thể tích khối hộp đã cho là
Thể tích khối lập phương tăng thêm bao nhiêu lần nếu độ dài cạnh của nó tăng gấp hai ?
Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Cho góc hợp bởi (A’BC) và mặt đáy là 30. Thể tích khối lăng trụ ABC.A’B’C’ là:
Cho lăng trụ đứng
có đáy ABC là tam giác vuông tại A; 
. Biết cạnh bên của lăng trụ bằng
. Thể tích khối lăng trụ là :
Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông cân tại A , BC=a2, A'B tạo với đáy một góc bằng 600 . Thể tích của khối lăng trụ bằng
Cho khối lăng trụ có diện tích s quy hoạnh đáy bằng
, khoảng chừng cách giữa hai đáy của lăng trụ bằng 
. Tính thể tích 
của khối lăng trụ
Cho lăngtrụ tam giácđều
cócạnhđáybằng
và
. Tínhthểtích
củakhốilăngtrụđãcho.
Đường kính của một hình cầu bằng cạnh của một hình lập phương. Thể tích của hình lập phương gấp thể tích hình cầu:
Cho hình hộp chữ nhật ABCD. A′B′C′D′ có AB=a, AD=a2 , mặt phẳng ABC′D′ tạo với mặt phẳng đáy góc 45° . Thể tích khối hộp chữ nhật đó là
Cho lăngtrụtamgiácđều
cócạnhđáybằng
là trọngtâmtamgiác
và
Thểtíchcủakhốilăngtrụ
bằng
Cho hình lăng trục
có đáy là tam giác ABC cân tại A, 
là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng 
Góc giữa 
và mặt thẳng 
bằng 
Tính thể tích V của khối lăng trụ 
Cho hình lăng trụ đứng
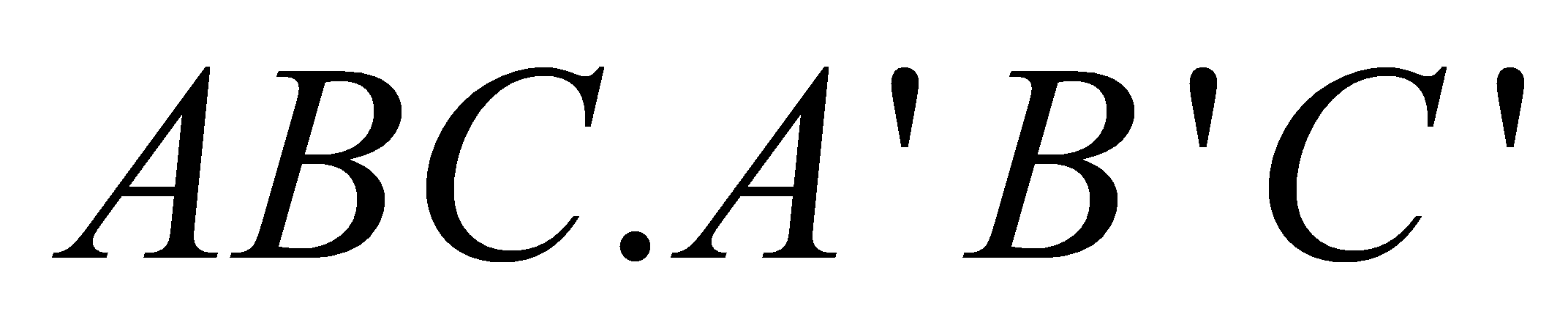có đáy
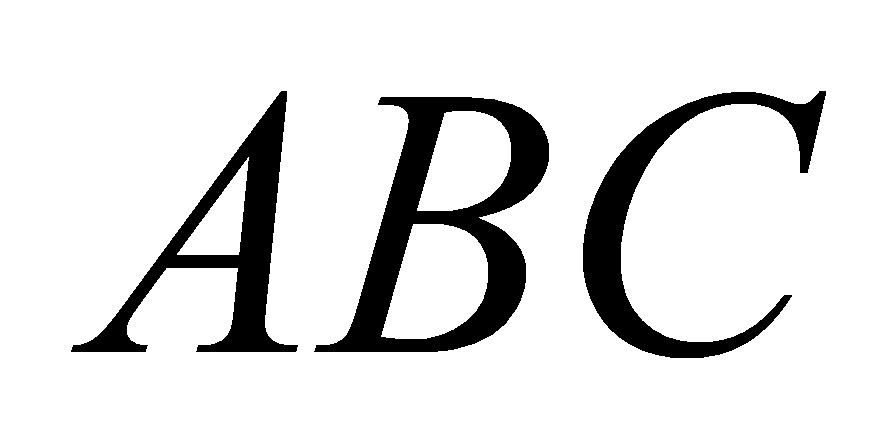là tam giác vuông tại 
, 
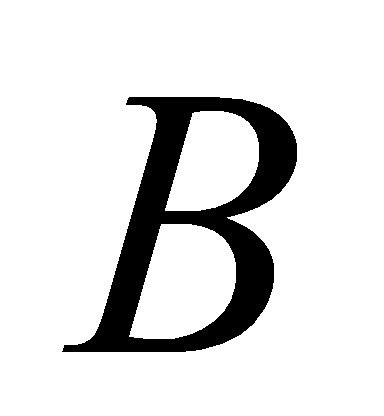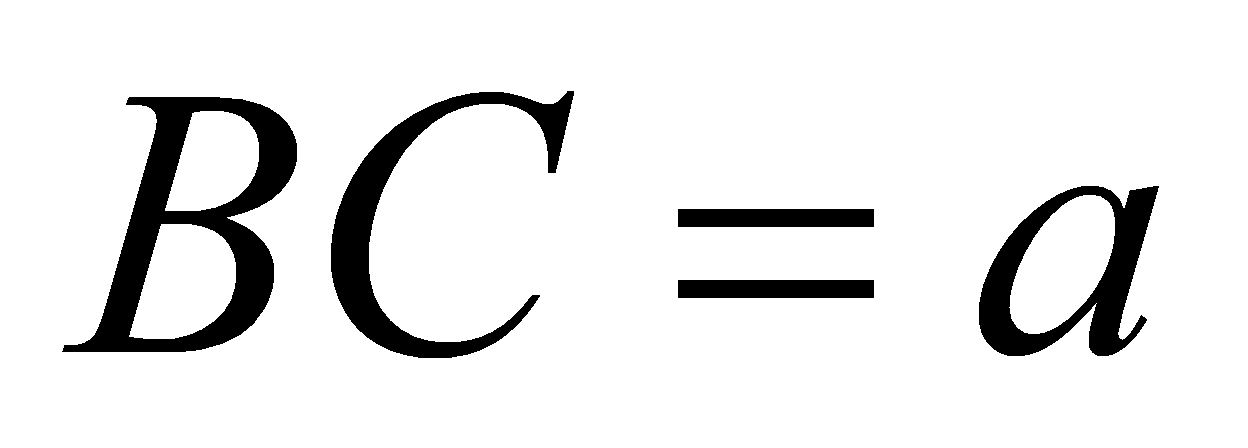, mặt phẳng 
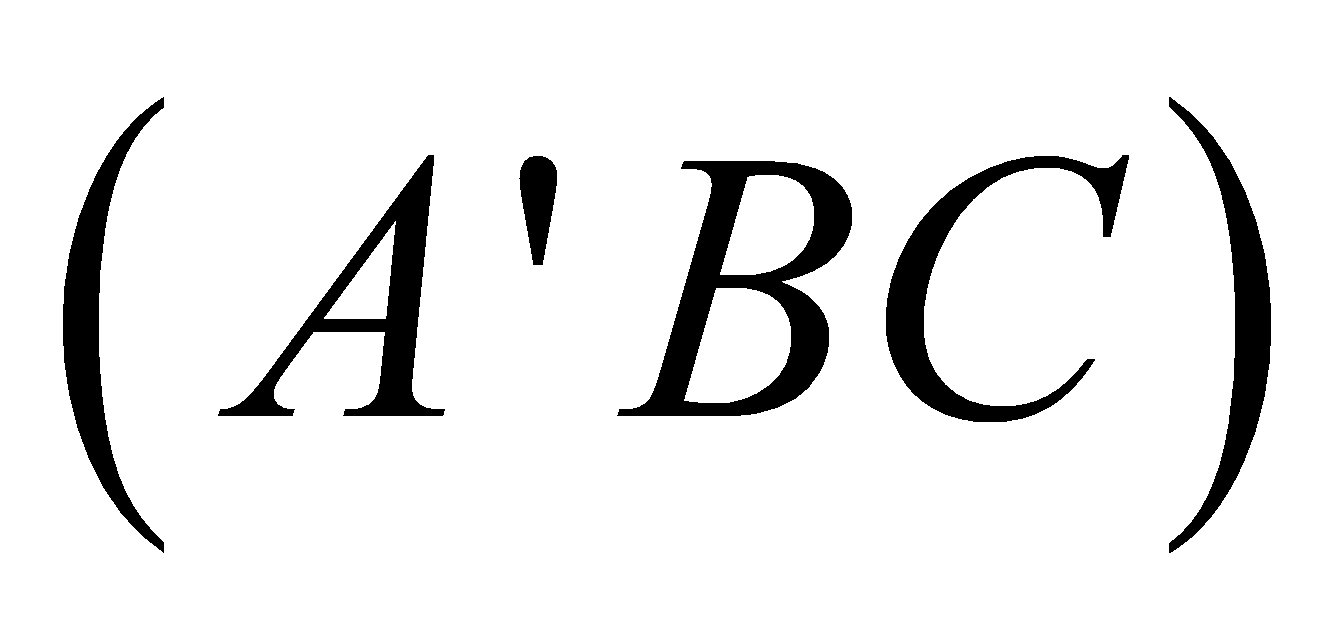tạo với đáy một góc 
và tam giác 
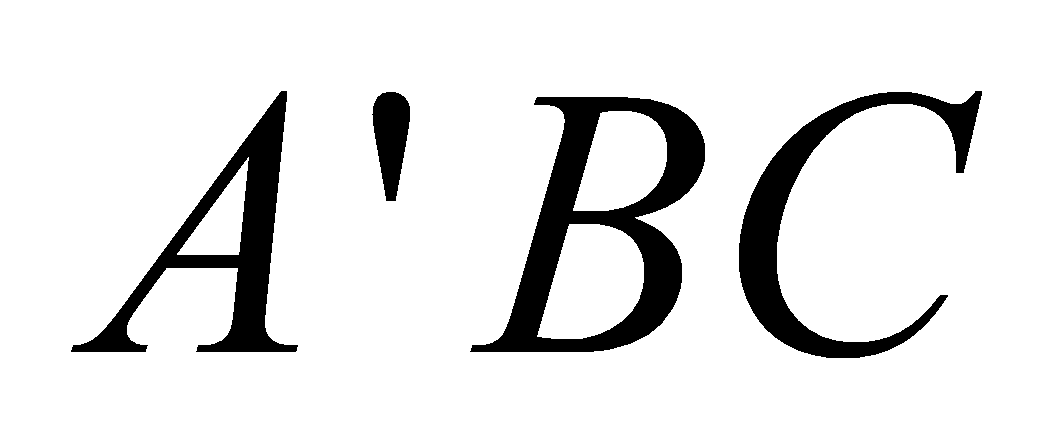có diện tích s quy hoạnh bằng 
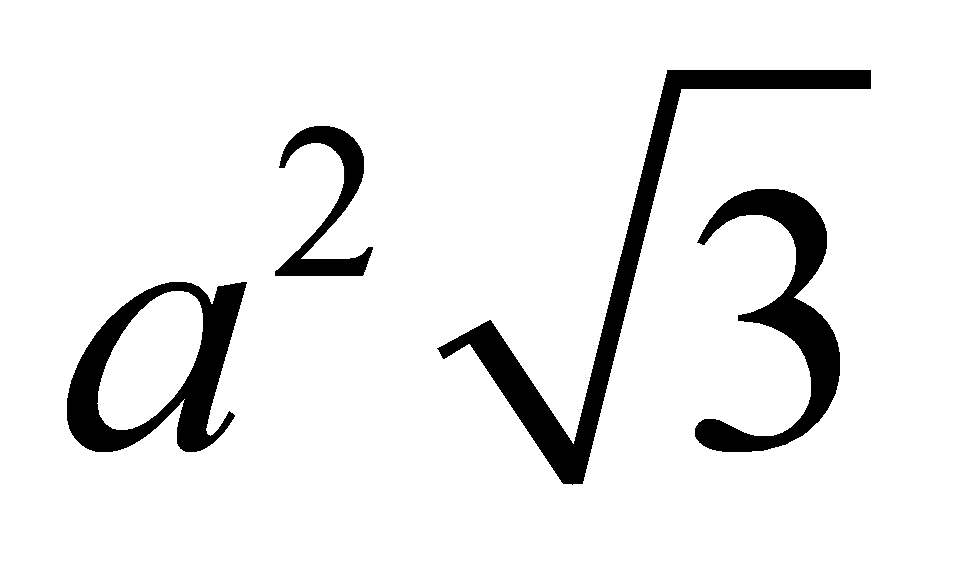. Tínhthểtíchkhốilăngtrụ
.
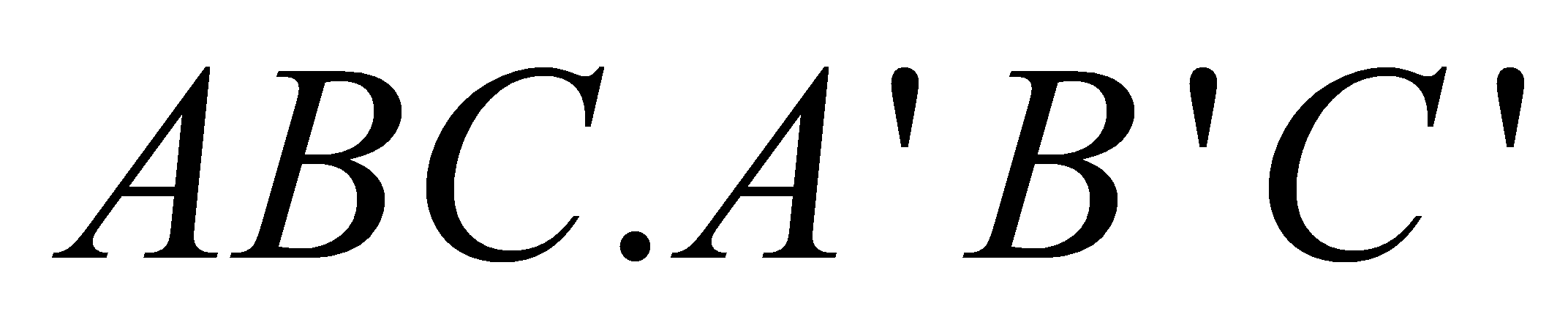Cho hình hộp đứng ABCD.A’B’C’D’ có đáy ABCD là hình thoi canh bằng a, góc 
và cạnh bên 
. Thể tích của khối hộp ABCD.A’B’C’D’là:
Thể tích của khối lăng trụ có diện tích s quy hoạnh đáy bằng
và độ cao bằng 
tính bằng công thức
Cho hình lăng trụ ABC.A’B’C’, đáy ABC có
. Cạnh bên phù phù hợp với mặt phẳng đáy góc 
và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC=3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng: 
Cho hình lăng trụ
có những mặt bên là hình vuông vắn cạnh 
Tính theo 
thể tích V của khối lăng trụ 
Cho lăng trụ tam giác đều
có diện tích s quy hoạnh đáy bằng 
. Mặt phẳng 
phù phù hợp với mặt phẳng đáy một góc
. Tính thể tích khối lăng trụ 
.
Cho lăng trụđứng tam giác đều ABC.A’B’C’, cócạnh đáy bằng a, đường chéo BC’của mặt bên (BCC’B’) tạo với mặt phẳng (ABB’A’) một góc 
. Thểtích khối lăng trụABC.A’B’C’theo a.
Cho khối lăng trụ đứng, mặt phẳng
đi qua 
và những trung điểm của 
, 
chia khối lăng trụ 
thành hai khối đa diện có tỷ số thể tích bằng 
với 
Tìm 
.
Cho hình lăng trụ tứ giác đều
có cạnh đáy bằng 
, đường chéo 
tạo với mặt bên 
một góc 
. Thể tích khối lăng trụ 
bằng :
Cho một tấm nhôm hình chữ nhật ABCD biết
. Ta gập tấm nhôm theo 2 cạnh MN và PQ vào phía trong đến khi AB và DC trùng nhau như hình vẽ, để được một hình lăng trụ khuyết 2 đáy. Tìm x để thể tích khối lăng trụ lớn số 1: 
Cho hìnhhộpchữ nhật ABCD.A’B’C’D’ có
. Biếtthể tíchhìnhcầungoạitiếptứ diện ABCD’ là 
. Tínhthể tích V củahìnhhộpchữ nhật ABCD.A’B’C’D’ .
Cho lăng trụđứng ABC.A’B’C’ cóđáy là tam giác cân,
, 
. Mặt phẳng 
tạo với mặt đáy góc 
. Tính thể tích lăng trụ ABC.A’B’C’.
Thể tích của khối lăng trụ có diện tích s quy hoạnh đáy bằng
và độ cao bằng
là
Khốilăngtrụtứgiácđềuvớiđộdàicạnhbênkhácđộdàicạnhđáycóbaonhiêumặtphẳngđốixứng?
Cho hình lăng trụ
có đáy 
là tam giác vuông tại 
góc hợp bởi đường thẳng 
và mặt phẳng 
bằng 
hình chiếu vuông góc của 
lên mặt phẳng 
trùng với trọng tâm của tam giác 
Tính thể tích khối lăng trụ 
Khi tăng độ dài tất cả những cạnh của một khối hộp chữ nhật lên gấp hai thì thể tích khối hộp tương ứng sẽ:
Cho hình hộp đứng ABCD A'B'C'D' cóđáy ABCD là hình thoi cạnh a và
biết AB' phù phù hợp với đáy (ABCD) một góc 
. Tính thể tích của khối hộp đó.
Cho hình trụ có bán kính đáy bằng
và độ cao bằng 
. Tính thể tích 
của khối lăng trụ tam giác đều nội tiếp hình trụ đã cho.
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, gọi I là trung điểm BC, góc giữa A’I và mặt phẳng (ABC) bằng
. Thể tích của khối lăng trụ ABC.A’B’C’ là:
Cho hình lăng trụABC.A’B’C’, đáy ABC có
, 
. Cạnh bên phù phù hợp với mặt phẳng đáy góc 
vàmặt phẳng 
vuông góc với mặt phẳng 
. Điểm H trên cạnh BC sao cho 
vàmặt phẳng 
vuông góc với mặt phẳng 
. Thểtích khối lăng trụABC.A’B’C’là
Cho khối lăng trụ đứng tam giác 
có đáy là một tam giác vuông cân tại 
, 
, góc giữa 
và mặt phẳng 
bằng 
. Thể tích khối lăng trụ 
là
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên
tạo với đáy một góc bằng 45. Thể tích khối lăng trụ bằng:
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác cân tại A,
, hình chiếu của A’ lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC, cạnh bên 
. Thể tích của khối lăng trụ là ?
Cho hình chữ nhật
có 
, 
. Gọi 
, 
là những điểm trên những cạnh 
, 
sao cho 
, 
. Khi quay quanh 
, những đường gấp khúc 
, 
sinh ra những hình trụ có diện tích s quy hoạnh toàn phần lần lượt là 
, 
. Tính tỉ số 
.
Cho khối hộp chữ nhật 
có những cạnh 
; 
; 
. Thể tích của khối hộp đó là:
Cho lăng trụ tam giác đều
có cạnh đáy bằng 
và 
. Khi đó thể tích của khối lăng trụ trên sẽ là:
Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên A’B tạo với đáy một góc 450. Thể tích khối lăng trụ ABC.A’B’C’ là:
Cho hìnhlăng trụtam giác
hoàn toàn có thể tích là 
và độ dài cạnh bên 
đơn vị. Cho điểm 
thuộc cạnh 
sao cho 
. Các điểm 
, 
lần lượt thuộc cạnh 
, 
sao cho 
, ở đó 
là những số thực dương thỏa mãn 
Biết rằng thể tích của khối đa diện 
bằng 
Giá trị của 
bằng:
Một số thắc mắc khác hoàn toàn có thể bạn quan tâm.
Tính hiệu chu vi của hình tứ giác ABCD và hình tam giác MNP trong hình vẽ sau:
Những học trò nào của giáo sư Vàng Anh tham gia cuộc thi?
Tìm độ dài cạnh không đủ của hình tam giác trong hình sau, biết chu vi của nó là 367cm.
Nhờ đâu Bết-tô-ven có cảm hứng để sáng tác bản xô-nát Ánh trăng?
Tìm độ dài cạnh hình tam giác không đủ trong hình sau, biết chu vi của nó là 608cm.
Vì sao cô nàng và người cha vô cùng ngạc nhiên?
Tính độ dài đường gấp khúc ABCD trong hình vẽ sau:
Vì sao trong người đàn ông trào dâng lên một niềm xúc động?
Em hãy cho biết thêm thêm bạn Duy thực hiện phép cộng như dưới đây là đúng hay sai, nếu sai thì bạn thực hiện sai từ bước nào ?
Đứng bên hiên chạy cửa số, người đang ông tình cờ thấy điều gì?
